Swing Twist Decomposition to Offset Parent Matrix

Decomposing a rotation into separate swing and twist components has many useful applications. Maya's pose interpolator toolset allows shapes to be driven with isolated twist and/or swing components of rotations. This allows a corrective shape in the pectorals driven by the raising of the arm to be independent from the twist motion of the arm. Also, the twist component can be used to drive twist joints more reliably than the euler twist axis by itself, as demonstrated in the video below.

In this post, I'll will explain how to create a swing/twist rotation decomposition to drive helper joints using Maya 2020's new offsetParentMatrix attribute.

First, we'll need a basic understanding of quaternions. I recommend the videos by 3Blue1Brown:

After playing with the interactive video here, we can see that the x, y, and z components of the quaternion control the axes of rotation (i, j, k in the interactive video). If we isolate the x, y, or z components, we end up with the rotation around the respective x, y, or z axis:

MQuaternion twist(rotation);

// Get the reference twist vector
switch (twistAxis) {
  case 0:  // X axis
    twist.y = 0.0;
    twist.z = 0.0;
    break;
  case 1:  // Y axis
    twist.x = 0.0;
    twist.z = 0.0;
    break;
  case 2:  // Z axis
    twist.x = 0.0;
    twist.y = 0.0;
    break;
}
twist.normalizeIt();

This means that we need the local rotation of the driver transform in order to calculate the twist. We could just use the driver.matrix attribute in our calculation, but I am going to add some complexity to make it a bit more robust. The problem with using driver.matrix is that it doesn't take into account joint orient or rotate axis. I want the solution to work whether joint orient is being used or not. This allows the math to transfer to other packages such as game engines. Joint orient is strictly a Maya paradigm. To get the local matrix including the effects of joint orient, I'll use:

There is a problem with using just the local matrix though. I want the driver joints resting rotation to be the identity swing and twist rotations in the system. If the driver joint contains joint orient or local rotations at bind time, I won't have an identity quaternion at rest. To account for this, I need to remove any local rest rotations to make sure the bind-time rotation is the identity quaternion:

// restMatrix is the stored local matrix at creation time
MMatrix localMatrix = matrix * restMatrix.inverse();
MQuaternion rotation = MTransformationMatrix(localMatrix).rotation();

At this point we have the decomposed twist quaternion. Calculating the swing component now is easy.

$$rotation = twist * swing$$

We know the full rotation, and we know the twist, so solving for swing:

$$swing = twist^{-1} * rotation$$

MQuaternion swing = twist.inverse() * rotation;

We now have the decomposed swing and twist components of the rotations. But what if we don't want the full twist or the full swing? Or what if we want the inverted twist? In the video at the top of this post, since the shoulder twist joints are parented to the shoulder joints, I want to remove the effects of the main shoulder joint twisting so I used -75% of the of the shoulder twist to drive the twist joint. We can scale and interpolate the decomposed swing and twist components by slerping them:

if (twistWeight < 0.0f) {
  twist.invertIt();
  twistWeight = -twistWeight;
}
if (swingWeight < 0.0f) {
  swing.invertIt();
  swingWeight = -swingWeight;
}

// Scale by the input weights
MQuaternion rest;
swing = slerp(rest, swing, swingWeight);
twist = slerp(rest, twist, twistWeight);

Now we have the scaled and/or inverted swing and twist rotations. To create the final matrix, we need to combine them back into a single rotation. And since we will be driving the offsetParentMatrix of the driven node, we convert to a matrix.

MQuaternion outRotation = twist * swing;
MMatrix outMatrix = outRotation.asMatrix();

There is a problem though. OffsetParentMatrix is the offset from the parent. The node we want to drive may not have its twist axis perfectly aligned with its parents twist axis. For example, if we drive a forearm twist joint from the wrist, the wrist may be slightly bent off the forearm axis at bind time. If the decomposed rotation matrix that we calculated is applied now, the twist will occur along the parents twist axis and not the driven nodes twist axis. To fix this we need to add the local rest offset to the rotation:

// targetRestMatrix is the stored (target.worldMatrix * target.parentInverseMatrix) at creation time
MQuaternion outRotation = twist * swing;
MMatrix outMatrix = outRotation.asMatrix() * targetRestMatrix;

We now have the final matrix we can connect to the target nodes offsetParentMatrix. However, there is one last issue. Any local transformation values on the driven node get applied before the offsetParentMatrix:

$$xform = local * offset * parent$$

Since we are calculating rotations in the offsetParentMatrix, if the joint has any values in tx, ty, tz, it will cause the joint to rotate off axis. Also since the offsetParentMatrix will contain translation values, we will end up with a double transform. The solution is just to zero out the local channels once the network is setup:

std::string attributes[] = {"translateX",
                            "translateY",
                            "translateZ",
                            "rotateX",
                            "rotateY",
                            "rotateZ"
                            "jointOrientX",
                            "jointOrientY",
                            "jointOrientZ"};
for (auto attribute : attributes) {
  MPlug plug = fnDriven.findPlug(attribute.c_str(), false, &status);
  if (!MFAIL(status)) {
    dgMod_.newPlugValueDouble(plug, 0.0);
  }
}

See the full source code on my GitHub

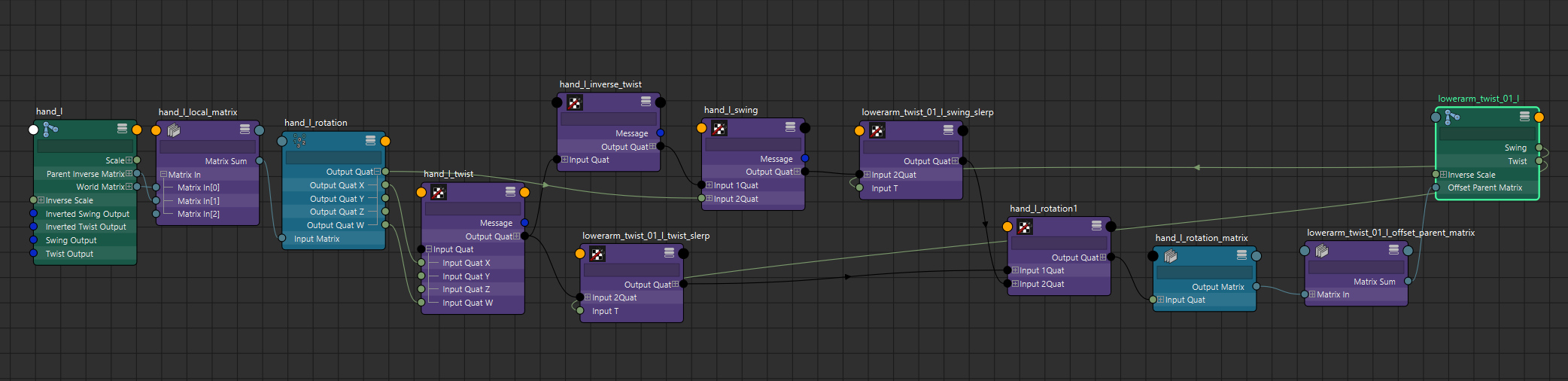
If you don't want to use a compiled plug-in, you can still create this setup with vanilla nodes. I have scripted the setup and you can also view it on my GitHub. I won't list the script in this post because it is a bit long. But all the math and quaternion operations described in this post are available as vanilla maya nodes. Note at the time of this writing, some of the documentation in the Python script is out of date and the integration with the UI and option box needs updating. That will get updated shortly…hopefully.

Node Network