By default Maya does not ship with any nodes to calculate trig functions. If you want to use a plug-in, you can use the great plug-in Maya Math Nodes written by Serguei Kalentchouk. If you want or have to use default Maya, there is still hope. I recently added trig function support to dge, my library that converts string math equations to Maya node networks. Using math and trig knowledge, we can recreate these functions with the nodes that come with Maya.

sin

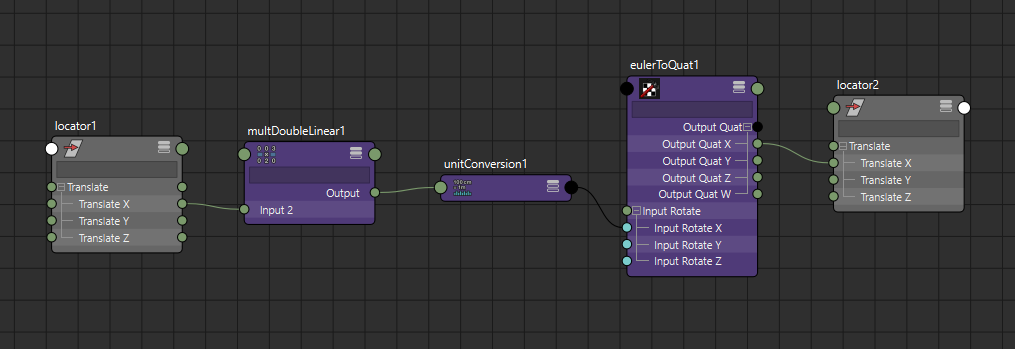
Looking at the math to convert euler angles to quaternions, we can see setting the rotate X angle by itself sets the X component of the quaternion to

$$\sin\left(\cfrac{\psi}{2}\right)$$

Using an eulerToQuat node which ships with Maya in the quatNodes plug-in, we can replicate this math:

def sin(x):
    cmds.loadPlugin("quatNodes", qt=False)
    mdl = cmds.createNode("multDoubleLinear")
    cmds.setAttr("{}.input1".format(mdl), 2 * 57.2958)  # To degrees
    if isinstance(x, string_types):
        cmds.connectAttr(x, "{}.input2".format(mdl))
    else:
        cmds.setAttr("{}.input2".format(mdl), x)
    quat = cmds.createNode("eulerToQuat")
    cmds.connectAttr("{}.output".format(mdl), "{}.inputRotateX".format(quat))
    return "{}.outputQuat.outputQuatX".format(quat)

cos

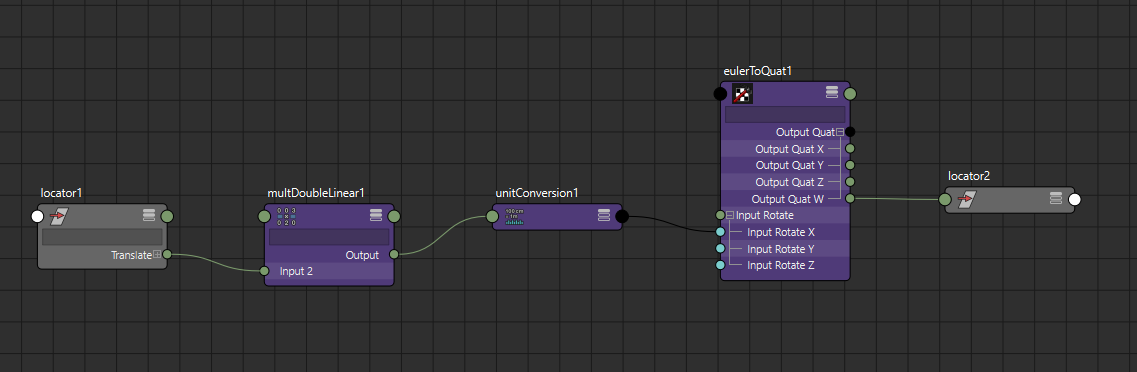
Cosine like sine can also be calculated using an eulerToQuat node. Setting the rotate X angle by itself, sets the W component of the quaternion to

$$\cos\left(\cfrac{\psi}{2}\right)$$

def cos(x):
    cmds.loadPlugin("quatNodes", qt=False)
    mdl = cmds.createNode("multDoubleLinear")
    cmds.setAttr("{}.input1".format(mdl), 2 * 57.2958)  # To degrees
    if isinstance(x, string_types):
        cmds.connectAttr(x, "{}.input2".format(mdl))
    else:
        cmds.setAttr("{}.input2".format(mdl), x)
    quat = cmds.createNode("eulerToQuat")
    cmds.connectAttr("{}.output".format(mdl), "{}.inputRotateX".format(quat))
    return "{}.outputQuat.outputQuatW".format(quat)

tan

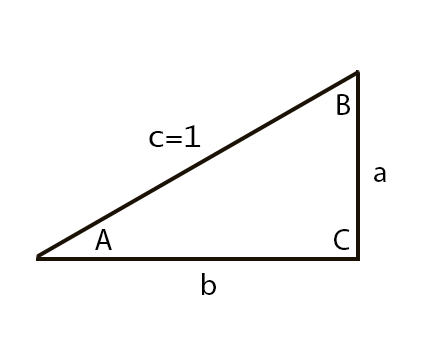
To calculate tangent we'll use the Law of Sines and solve for an ASA triangle.

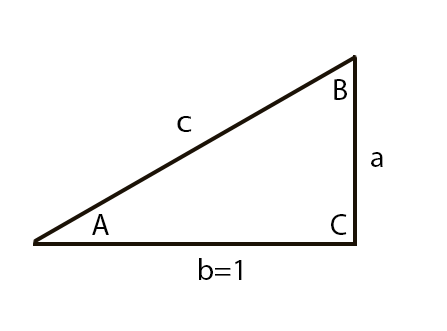
We know that the tangent of an angle is the length of the opposite edge over the length of the adjacent edge in a right triangle. If we assume the length of the adjacent edge is 1, we then just need to find the length of the opposite edge (a in the image). We can calculate the length of the opposite edge using the Law of Sines:

$$\cfrac{a}{\sin\left(A\right)} = \cfrac{b}{\sin\left(B\right)}$$

Since b is length 1, we solve for a:

$$a = \cfrac{\sin\left(A\right)}{\sin\left(B\right)}$$

To solve this equation, we need to find angle B. Since the angles of a triangle add up to 180 degrees and we know angle C is 90 degrees, that means

$$A + B = 90$$

or

$$B = \cfrac{\pi}{2} - A$$

We can hook in all of our known values to solve for length a which will be the tangent of angle A.

def tan(x):
    half_pi = math.pi * 0.5
    c = dge("{} - x".format(half_pi), x=x)
    return dge("sin(x) / sin(c)", x=x, c=c)

asin

For the inverse trig functions we'll use the angleBetween node to calculate our final result. This means we need to calculate the vectors that input to the angleBetween node. Sin is opposite over hypotenuse, so if we assume the hypotenuse has length 1, we can simplify our calculation:

$$\arcsin\left(a\right) = A$$

This means the asin of whatever value we want to calculate is angle A or the angle between edges b and c so we need to calculate those vectors to enter in to the angleBetween node. Using the Pythagorean Theorem

$$a^2 + b^2 = c^2$$

$$b = \sqrt{c^2 - a^2}$$

Since we assume the hypotenuse is length 1:

$$b = \sqrt{1 - a^2}$$

Since a is the value we are providing, we can now populate the vectors of the angleBetween node.

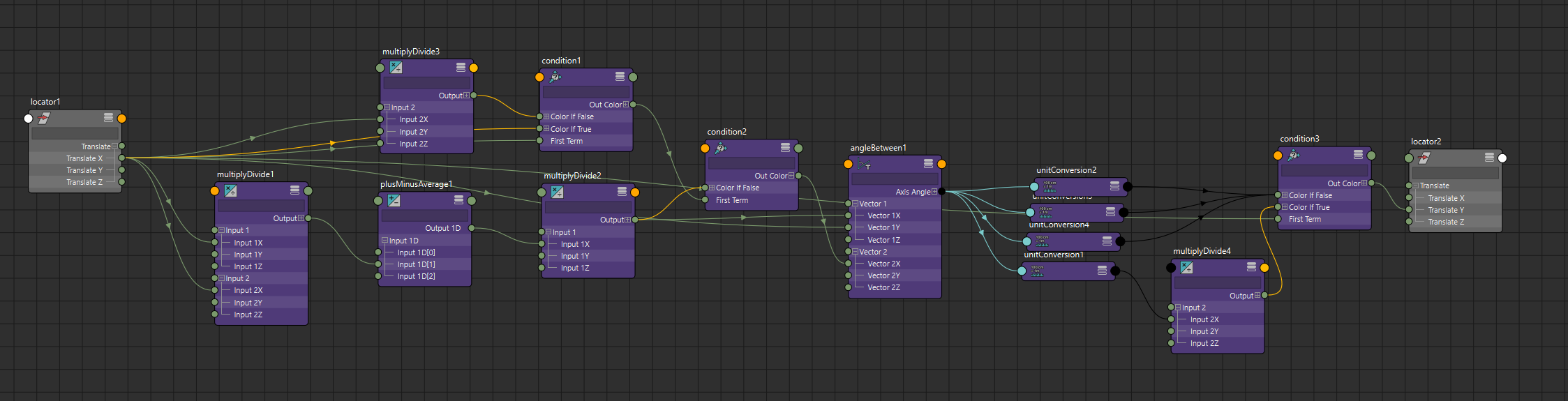
def asin(x):
    angle = cmds.createNode("angleBetween")
    for attr in ["{}{}".format(i, j) for i in [1, 2] for j in "XYZ"]:
        cmds.setAttr("{}.vector{}".format(angle, attr), 0)

    if isinstance(x, string_types):
        cmds.connectAttr(x, "{}.vector1Y".format(angle))
    else:
        cmds.setAttr("{}.vector1Y".format(angle), x)
    result = dge("sqrt(1.0 - x*x)", x=x)
    cmds.connectAttr(result, "{}.vector1X".format(angle))
    dge("y=abs(x) == 1.0 ? 1.0 : r", y="{}.vector2X".format(angle), x=x, r=result)
    return dge("x < 0 ? -y : y", x=x, y="{}.axisAngle.angle".format(angle))

We do have to special-case the end of the domain of asin (-1 and 1). Since those values end up resulting in 0 with this technique, we would end up with a 0 vector and the angleBetween node would return 0. To account for this, we explicitly check for those values and set angleBetween vectors to return 90 degrees. Also since the angleBetween node always returns positive values, we flip the sign depending on the sign of the input value.

acos

acos is similar to asin. Cos is adjacent over hypotenuse so if we assume the hypotenuse has length 1:

$$\arccos\left(b\right) = A$$

Like asin, we need to calculate the vectors b and c to pass to the angle between node. b is easy because we are the ones providing that value. b is also the X axis value of the c vector so we just need to calculate a for the Y axis value of the c vector. Again with the Pythagorean Theorem and since we assume the hypotenuse is length 1:

$$a = \sqrt{1 - b^2}$$

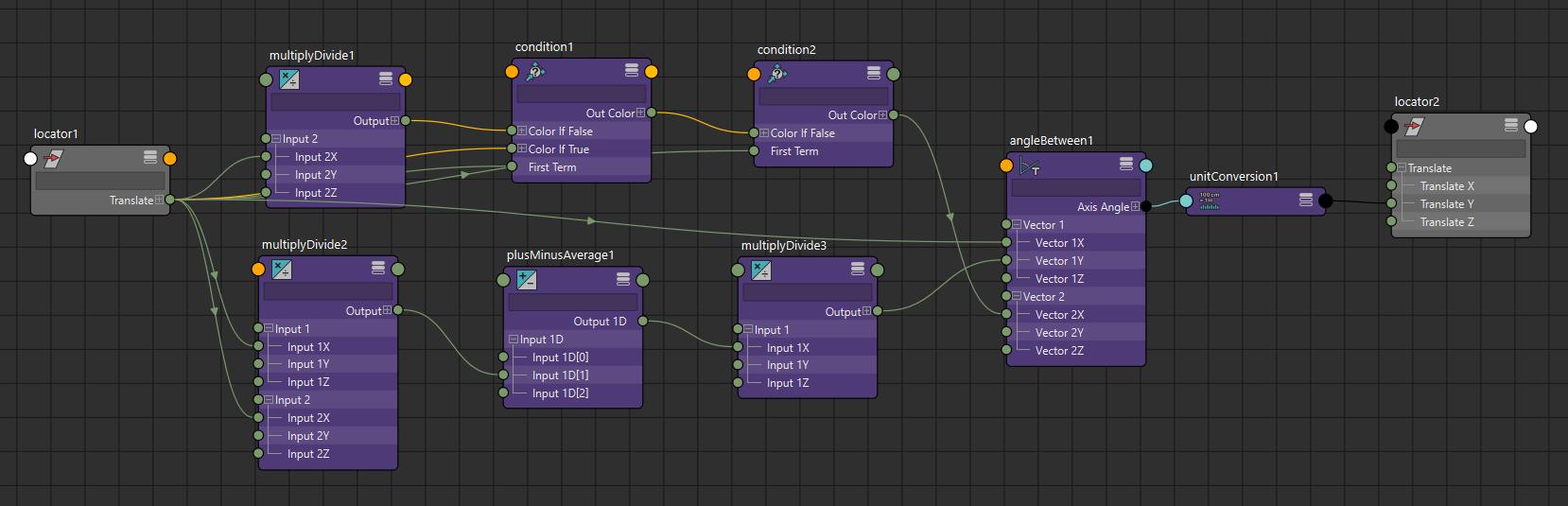
def acos(x):
    angle = cmds.createNode("angleBetween")
    for attr in ["{}{}".format(i, j) for i in [1, 2] for j in "XYZ"]:
        cmds.setAttr("{}.vector{}".format(angle, attr), 0)

    if isinstance(x, string_types):
        cmds.connectAttr(x, "{}.vector1X".format(angle))
        dge("y = x == 0.0 ? 1.0 : abs(x)", y="{}.vector2X".format(angle), x=x)
    else:
        cmds.setAttr("{}.vector1X".format(angle), x)
        cmds.setAttr("{}.vector2X".format(angle), math.fabs(x))
    dge("y = sqrt(1.0 - x*x)",
        y="{}.vector1Y".format(angle),
        x=x)
    return "{}.axisAngle.angle".format(angle)

Like asin, there is a special case value. For acos, if the input value is 0, we would get a zero vector and the angleBetween node would return 0 instead of the correct value of 90 degrees. We put in a conditional for the 0 value make sure the vector going in to the angleBetween node doesn't turn in to a zero vector.

atan

For atan, we use a similar technique as the other inverse functions. Tan is opposite over adjacent, so this time we will assume the adjacent side has length 1 which simplifies the calculation:

$$\arctan\left(a\right) = A$$

Since we assume the adjacent side b has length 1, and a is the value we are providing, we already have all the values we need to calculate the vectors for the angleBetween node:

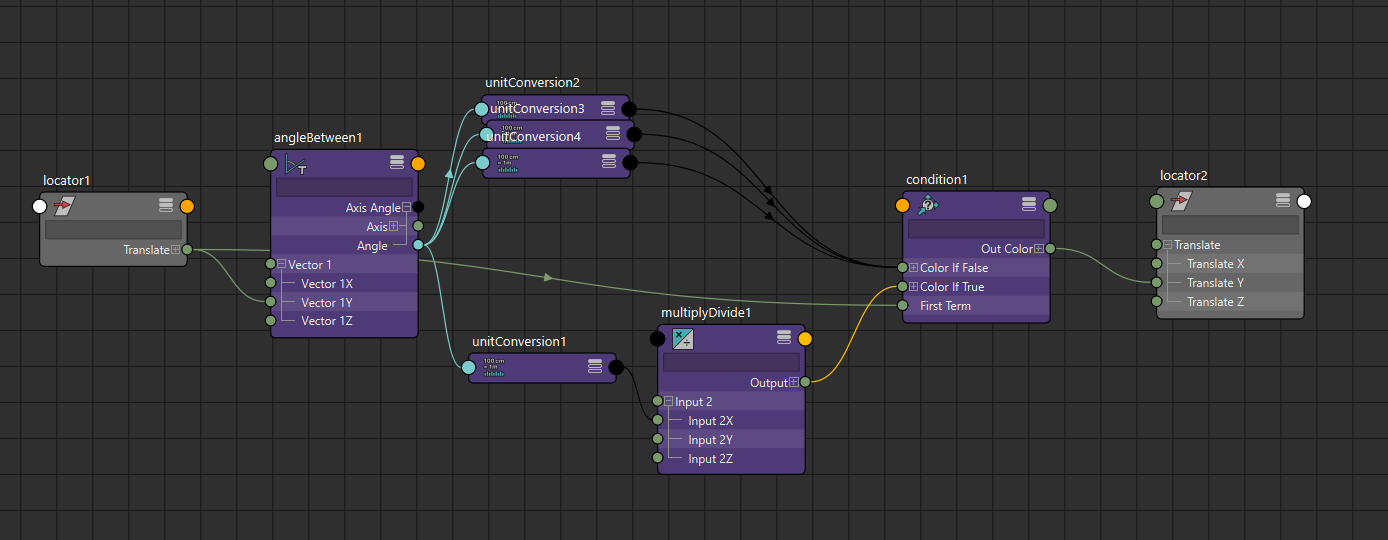
def atan(x):
    angle = cmds.createNode("angleBetween")
    for attr in ["{}{}".format(i, j) for i in [1, 2] for j in "XYZ"]:
        cmds.setAttr("{}.vector{}".format(angle, attr), 0)
    cmds.setAttr("{}.vector1X".format(angle), 1)
    cmds.setAttr("{}.vector2X".format(angle), 1)

    if isinstance(x, string_types):
        cmds.connectAttr(x, "{}.vector1Y".format(angle))
    else:
        cmds.setAttr("{}.vector1Y".format(angle), x)
    return dge("x < 0 ? -y : y", x=x, y="{}.axisAngle.angle".format(angle))

Like asin, since the angleBetween node always returns positive values, we flip the sign depending on the sign of the input value.

Some of the node networks are admittedly more complex than desired but they do allow you to access trig functions without third-part plug-ins. I would never want to set up these networks by hand as that would quickly drive me crazy. That is the whole point of my dge library. If you are worried about the absolute best performance and trying to minimize node count, use Maya Math Nodes. If you want to stick with vanilla Maya, you can either use expressions or the techniques described in this post.