In my previous post, I described how to create an RBF solver using regularized linear regression. While the solver works well for most independent input values, it does not work so well if we want to drive it with euler rotations. Euler rotations are susceptible to gimbal lock and can have multiple solutions for the same rotation.
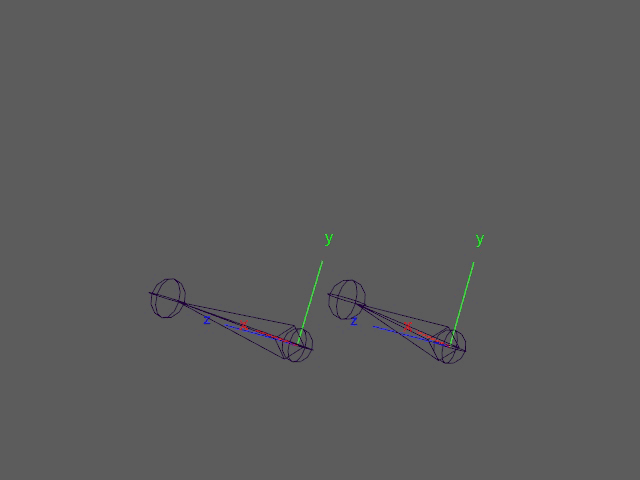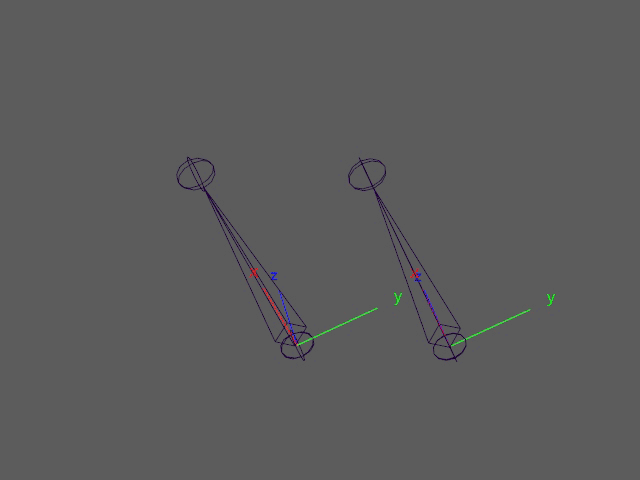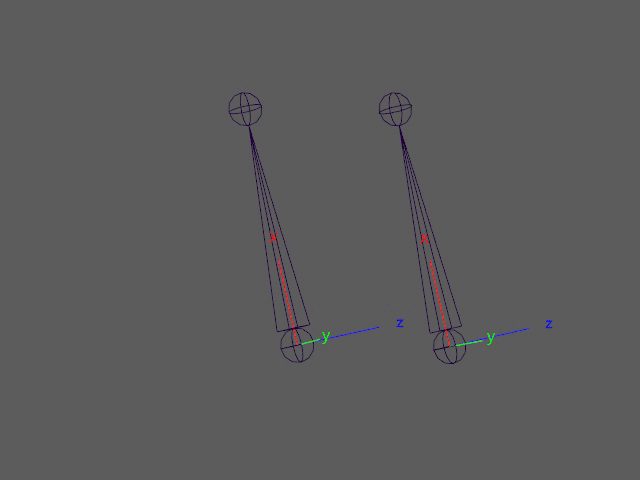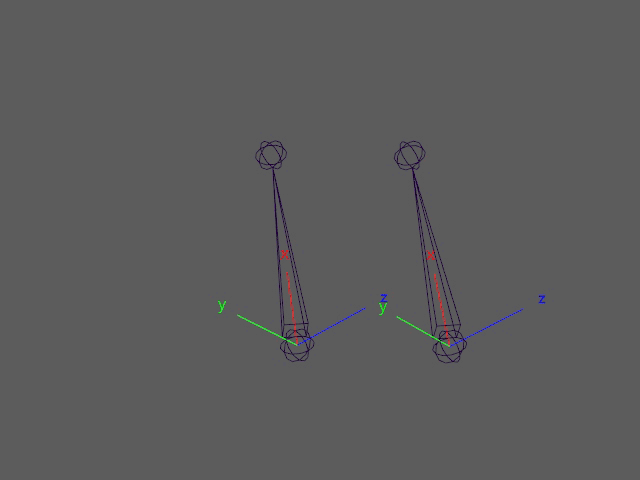
These two joints look like they have the same rotation. But looking at their animation curves tells a different story:
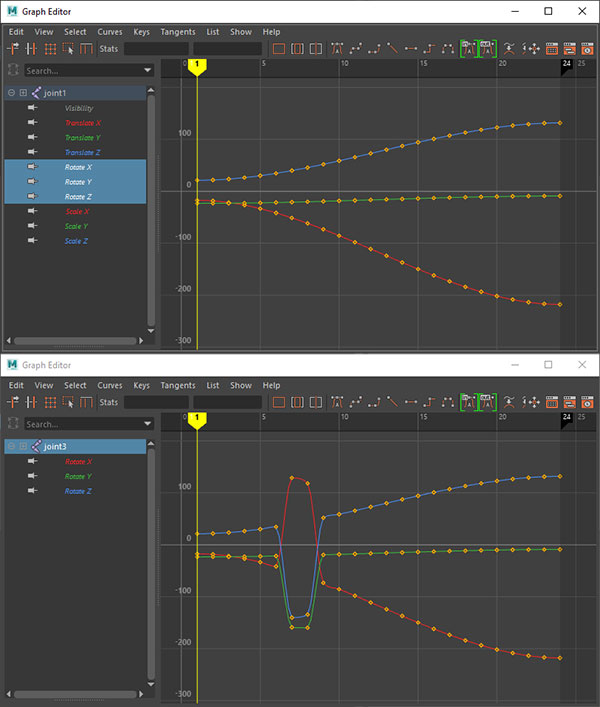
If the euler rotations were used to drive corrective shapes in this case, the shapes would twitch during those two frames. A more reliable approach is to use quaternion inputs. Quaternions are not able to fall into gimbal lock. While quaternions can also have multiple solutions for the same rotations (q and -q represent the same rotation), they provide a means to calculate a unique solution by calculating the angle difference between rotations. In the previous post, I described the feature matrix and corresponding distance matrix looking like the following.
$$ M = \begin{bmatrix} 0.5 & 0.2 & 0.7 & 0.1 \\ 0.1 & 0.9 & 0.3 & 0.2 \\ 0.9 & 0.8 & 0.3 & 0.5 \end{bmatrix}, M_d = \begin{bmatrix} 0.0 & 0.906 & 0.917 \\ 0.906 & 0.0 & 0.860 \\ 0.917 & 0.860 & 0.0 \end{bmatrix} $$
To add quaternion rotation support, we will also store quaternions in the feature matrix. For example, if we want to use two different rotations as input into our solver, the feature matrix would look like this:
$$ M = \begin{bmatrix} 0.5 & 0.2 & 0.7 & 0.1 & Q_{1a} & Q_{1b} \\ 0.1 & 0.9 & 0.3 & 0.2 & Q_{2a} & Q_{2b} \\ 0.9 & 0.8 & 0.3 & 0.5 & Q_{3a} & Q_{2b} \end{bmatrix} $$
Now we can't really calculate a euclidean distance of the scalar values and quaternions all combined. But what we can do is calculate the distance of the scalar values and the quaternion “distances” separately and then add them together. This basically turns our feature matrix into one matrix for the scalar values and one matrix for each quaternion input.
$$ M = \begin{bmatrix} 0.5 & 0.2 & 0.7 & 0.1 \\ 0.1 & 0.9 & 0.3 & 0.2 \\ 0.9 & 0.8 & 0.3 & 0.5 \end{bmatrix}, M_a = \begin{bmatrix} Q_{1a} \\ Q_{2a} \\ Q_{3a} \end{bmatrix} M_b = \begin{bmatrix} Q_{1b} \\ Q_{2b} \\ Q_{3b} \end{bmatrix} $$
To use RBF, we need values in terms of distance. We can calculate the angle difference between two quaternions with:
$$ \theta = \cos^{-1}\left(2 \cdotp dot(q_1, q_2)^2 - 1\right) $$
The benefit of this approach over cone-based methods is this takes into account the twist of the rotation. In code this would look like the following. Note we normalize the quaternion distance to a 0-1 range.
double quaternionDot(const MQuaternion& q1, const MQuaternion& q2) {
double dotValue = (q1.x * q2.x) + (q1.y * q2.y) + (q1.z * q2.z) + (q1.w * q2.w);
// Clamp any floating point error since this will go in to acos
if (dotValue < -1.0) {
dotValue = -1.0;
} else if (dotValue > 1.0) {
dotValue = 1.0;
}
return dotValue;
}
double quaternionDistance(MQuaternion& q1, MQuaternion& q2) {
double dot = quaternionDot(q1, q2);
return acos(2.0 * dot * dot - 1.0) / M_PI;
}
Calculating the distance matrices for each of our feature matrices now gives:
$$ M_d = \begin{bmatrix} 0.0 & 0.906 & 0.917 \\ 0.906 & 0.0 & 0.860 \\ 0.917 & 0.860 & 0.0 \end{bmatrix}, $$
$$ M_{da} = \begin{bmatrix} \Delta\left(Q_{1a}, Q_{1a}\right) & \Delta\left(Q_{1a}, Q_{2a}\right) & \Delta\left(Q_{1a}, Q_{3a}\right) \\ \Delta\left(Q_{2a}, Q_{1a}\right) & \Delta\left(Q_{2a}, Q_{2a}\right) & \Delta\left(Q_{2a}, Q_{3a}\right) \\ \Delta\left(Q_{3a}, Q_{1a}\right) & \Delta\left(Q_{3a}, Q_{2a}\right) & \Delta\left(Q_{3a}, Q_{3a}\right) \end{bmatrix} $$
$$ M_{db} = \begin{bmatrix} \Delta\left(Q_{1b}, Q_{1b}\right) & \Delta\left(Q_{1b}, Q_{2b}\right) & \Delta\left(Q_{1b}, Q_{3b}\right) \\ \Delta\left(Q_{2b}, Q_{1b}\right) & \Delta\left(Q_{2b}, Q_{2b}\right) & \Delta\left(Q_{2b}, Q_{3b}\right) \\ \Delta\left(Q_{3b}, Q_{1b}\right) & \Delta\left(Q_{3b}, Q_{2b}\right) & \Delta\left(Q_{3b}, Q_{3b}\right) \end{bmatrix} $$
Now we can just add all these matrices together to get a distance matrix between samples.
$$ M_D = M_d + \sum_{\mathclap{1\le i\le n}} M_{di} $$
if (inputQuatCount) {
std::vector<MatrixXd> mQuat(inputQuatCount);
for (int i = 0; i < inputQuatCount; ++i) {
mQuat[i].resize(sampleCount, sampleCount);
}
// Calculate rotation distances
for (int s1 = 0; s1 < sampleCount; ++s1) {
for (int s2 = 0; s2 < sampleCount; ++s2) {
for (int i = 0; i < inputQuatCount; ++i) {
MQuaternion& q1 = featureQuatMatrix_[s1][i];
MQuaternion& q2 = featureQuatMatrix_[s2][i];
double distance = quaternionDistance(q1, q2);
mQuat[i](s1, s2) = distance;
}
}
}
// Add rotational distances to main distance
for (auto& rd : mQuat) {
m += rd;
}
// Normalized float distance is 0-1, rotational distances are 0-1
// Added together they are 0-(inputQuatCount+1)
// Scale back to 0-1 range
double scalar = inputCount > 0 ? 1.0 / static_cast<double>(inputQuatCount + 1)
: 1.0 / static_cast<double>(inputQuatCount);
m *= scalar;
}
Notice at the end we renormalize the distance matrix to work well with the RBF radius parameter. This implementation supports scalar values alone, quaternion values alone, or a mix of the two as inputs which is why the normalization depends on whether a scalar feature matrix exists.
Another benefit of using quaternions as input into the RBF is when combined with Swing Twist Decomposition, we can now drive output values with just the swing and/or twist of a rotation.

To see the implementation of the full node, refer to my Github.